Feature selection using forward selection
Contents
Feature selection using forward selection#
Reducing the number of features we use can have three benefits:
Simplifies model explanation
Model fit may be improved by the removal of features that add no value
Model will be faster to fit
In this notebook we will use a model-based approach whereby we incrementally add features that most increase model performance (we could use simple accuracy, but in this case we will use ROC Area Under Curve as a more thorough analysis of performance).
Two key advantages of this method are:
It is relatively simple.
It is tailored to the model in question.
Some key disadvantage of this method are:
It may be slow if there are many parameters (though the loop to select features could be limited in the number of features to select).
The selection of features may be dependent on model meta-parameters (such as level of regularisation).
The selection of features may not transfer between models (e.g. a model that does not allow for feature interactions may not detect features which do not add much value independently).
We will go through the following steps:
Download and save pre-processed data
Split data into features (X) and label (y)
Loop through features to select the feature that most increases ROC AUC
Plot results
https://scikit-learn.org/stable/modules/feature_selection.html#recursive-feature-elimination
# Hide warnings (to keep notebook tidy; do not usually do this)
import warnings
warnings.filterwarnings("ignore")
Load modules#
A standard Anaconda install of Python (https://www.anaconda.com/distribution/) contains all the necessary modules.
import numpy as np
import pandas as pd
# Import machine learning methods
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import auc
from sklearn.metrics import roc_curve
from sklearn.model_selection import StratifiedKFold
from sklearn.preprocessing import StandardScaler
Load data#
The section below downloads pre-processed data, and saves it to a subfolder (from where this code is run). If data has already been downloaded that cell may be skipped.
download_required = True
if download_required:
# Download processed data:
address = 'https://raw.githubusercontent.com/MichaelAllen1966/' + \
'1804_python_healthcare/master/titanic/data/processed_data.csv'
data = pd.read_csv(address)
# Create a data subfolder if one does not already exist
import os
data_directory ='./data/'
if not os.path.exists(data_directory):
os.makedirs(data_directory)
# Save data
data.to_csv(data_directory + 'processed_data.csv', index=False)
data = pd.read_csv('data/processed_data.csv')
# Make all data 'float' type
data = data.astype(float)
The first column is a passenger index number. We will remove this, as this is not part of the original Titanic passenger data.
# Drop Passengerid (axis=1 indicates we are removing a column rather than a row)
# We drop passenger ID as it is not original data
data.drop('PassengerId', inplace=True, axis=1)
Divide into X (features) and y (labels)#
We will separate out our features (the data we use to make a prediction) from our label (what we are truing to predict).
By convention our features are called X (usually upper case to denote multiple features), and the label (survive or not) y.
X = data.drop('Survived',axis=1) # X = all 'data' except the 'survived' column
y = data['Survived'] # y = 'survived' column from 'data'
Forward feature selection#
Define data standardisation function.
def standardise_data(X_train, X_test):
# Initialise a new scaling object for normalising input data
sc = StandardScaler()
# Set up the scaler just on the training set
sc.fit(X_train)
# Apply the scaler to the training and test sets
train_std=sc.transform(X_train)
test_std=sc.transform(X_test)
return train_std, test_std
The forward selection method:
Keeps a list of selected features
Keeps a list of features still available for selection
Loops through available features:
Calculates added value for each feature (using stratified k-fold validation)
Selects feature that adds most value
Adds selected feature to selected features list and removes it from available features list
This method uses a while lop to keep exploring features until no more are available. An alternative would be to use a for loop with a maximum number of features to select.
# Create list to store accuracies and chosen features
roc_auc_by_feature_number = []
chosen_features = []
# Initialise chosen features list and run tracker
available_features = list(X)
run = 0
number_of_features = len(list(X))
# Loop through feature list to select next feature
while len(available_features)> 0:
# Track and pront progress
run += 1
print ('Feature run {} of {}'.format(run, number_of_features))
# Convert DataFrames to NumPy arrays
y_np = y.values
# Reset best feature and accuracy
best_result = 0
best_feature = ''
# Loop through available features
for feature in available_features:
# Create copy of already chosen features to avoid original being changed
features_to_use = chosen_features.copy()
# Create a list of features from features already chosen + 1 new feature
features_to_use.append(feature)
# Get data for features, and convert to NumPy array
X_np = X[features_to_use].values
# Set up lists to hold results for each selected features
test_auc_results = []
# Set up k-fold training/test splits
number_of_splits = 5
skf = StratifiedKFold(n_splits = number_of_splits)
skf.get_n_splits(X_np, y)
# Loop through the k-fold splits
for train_index, test_index in skf.split(X_np, y_np):
# Get X and Y train/test
X_train, X_test = X_np[train_index], X_np[test_index]
y_train, y_test = y[train_index], y[test_index]
# Get X and Y train/test
X_train_std, X_test_std = standardise_data(X_train, X_test)
# Set up and fit model
model = LogisticRegression(solver='lbfgs')
model.fit(X_train_std,y_train)
# Predict test set labels
y_pred_test = model.predict(X_test_std)
# Calculate accuracy of test sets
accuracy_test = np.mean(y_pred_test == y_test)
# Get ROC AUC
probabilities = model.predict_proba(X_test_std)
probabilities = probabilities[:, 1] # Probability of 'survived'
fpr, tpr, thresholds = roc_curve(y_test, probabilities)
roc_auc = auc(fpr, tpr)
test_auc_results.append(roc_auc)
# Get average result from all k-fold splits
feature_auc = np.mean(test_auc_results)
# Update chosen feature and result if this feature is a new best
if feature_auc > best_result:
best_result = feature_auc
best_feature = feature
# k-fold splits are complete
# Add mean accuracy and AUC to record of accuracy by feature number
roc_auc_by_feature_number.append(best_result)
chosen_features.append(best_feature)
available_features.remove(best_feature)
# Put results in DataFrame
results = pd.DataFrame()
results['feature to add'] = chosen_features
results['ROC AUC'] = roc_auc_by_feature_number
Feature run 1 of 24
Feature run 2 of 24
Feature run 3 of 24
Feature run 4 of 24
Feature run 5 of 24
Feature run 6 of 24
Feature run 7 of 24
Feature run 8 of 24
Feature run 9 of 24
Feature run 10 of 24
Feature run 11 of 24
Feature run 12 of 24
Feature run 13 of 24
Feature run 14 of 24
Feature run 15 of 24
Feature run 16 of 24
Feature run 17 of 24
Feature run 18 of 24
Feature run 19 of 24
Feature run 20 of 24
Feature run 21 of 24
Feature run 22 of 24
Feature run 23 of 24
Feature run 24 of 24
Show results#
results
| feature to add | ROC AUC | |
|---|---|---|
| 0 | male | 0.766818 |
| 1 | Pclass | 0.833003 |
| 2 | Age | 0.843038 |
| 3 | SibSp | 0.848621 |
| 4 | Embarked_S | 0.853128 |
| 5 | CabinLetter_E | 0.856015 |
| 6 | CabinNumberImputed | 0.856436 |
| 7 | CabinLetter_F | 0.856244 |
| 8 | CabinLetter_D | 0.856363 |
| 9 | CabinLetter_T | 0.856470 |
| 10 | CabinLetterImputed | 0.856179 |
| 11 | CabinLetter_missing | 0.856205 |
| 12 | EmbarkedImputed | 0.855806 |
| 13 | Embarked_missing | 0.855806 |
| 14 | Fare | 0.855255 |
| 15 | CabinLetter_A | 0.854322 |
| 16 | CabinLetter_B | 0.853133 |
| 17 | CabinNumber | 0.852493 |
| 18 | AgeImputed | 0.851652 |
| 19 | CabinLetter_C | 0.850288 |
| 20 | CabinLetter_G | 0.849589 |
| 21 | Embarked_C | 0.847322 |
| 22 | Embarked_Q | 0.847428 |
| 23 | Parch | 0.846065 |
Plot results#
import matplotlib.pyplot as plt
%matplotlib inline
chart_x = list(range(1, number_of_features+1))
plt.plot(chart_x, roc_auc_by_feature_number,
label = 'ROC AUC')
plt.xlabel('Number of features')
plt.ylabel('Accuracy (ROC AUC)')
plt.legend()
plt.grid(True)
plt.show()
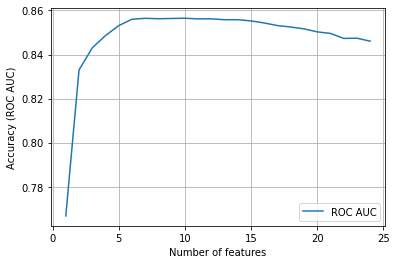
From the above results it looks like we could use just 5-7 features in this model. It may also be worth examining the same method using other performance scores (such as simple accuracy, or f1) in place of ROC AUC.
Note that accuracy of the model appears to decline with a greater number of features.