Explaining model predictions with Shapley values - Logistic Regression

Shapley values provide an estimate of how much any particular feature influences the model decision. When Shapley values are averaged they provide a measure of the overall influence of a feature.

Shapley values may be used across model types, and so provide a model-agnostic measure of a feature’s influence. This means that the influence of features may be compared across model types, and it allows black box models like neural networks to be explained, at least in part.

Here we will demonstrate Shapley values with logistic regression.

For more on Shapley values in general see Chris Molner’s excellent book chapter:

https://christophm.github.io/interpretable-ml-book/shapley.html

The shap package is installed if you have used the Titanic environment yasml file, but otherwise may be installed with pip install shap.

More information on the shap library, inclusiong lots of useful examples may be found at: https://shap.readthedocs.io/en/latest/index.html

Here we provide an example of using shap with logistic regression. Logistic regression is the model type which least needs an explainer but it provides a useful example for learning about shap as Shapley values may be compared with model coefficients.

Load data and fit model

Load modules

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
# Import machine learning methods
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
# Import shap for shapley values
import shap # `pip install shap` if neeed

Load data

The section below downloads pre-processed data, and saves it to a subfolder (from where this code is run). If data has already been downloaded that cell may be skipped.

Code that was used to pre-process the data ready for machine learning may be found at: https://github.com/MichaelAllen1966/1804_python_healthcare/blob/master/titanic/01_preprocessing.ipynb

download_required = True

if download_required:
    
    # Download processed data:
    address = 'https://raw.githubusercontent.com/MichaelAllen1966/' + \
                '1804_python_healthcare/master/titanic/data/processed_data.csv'
    
    data = pd.read_csv(address)

    # Create a data subfolder if one does not already exist
    import os
    data_directory ='./data/'
    if not os.path.exists(data_directory):
        os.makedirs(data_directory)

    # Save data
    data.to_csv(data_directory + 'processed_data.csv', index=False)

data = pd.read_csv('data/processed_data.csv')
# Make all data 'float' type
data = data.astype(float)

Divide into X (features) and y (labels)

We will separate out our features (the data we use to make a prediction) from our label (what we are truing to predict). By convention our features are called X (usually upper case to denote multiple features), and the label (survived or not) y.

# Use `survived` field as y, and drop for X
y = data['Survived'] # y = 'survived' column from 'data'
X = data.drop('Survived',axis=1) # X = all 'data' except the 'survived' column

# Drop PassengerId
X.drop('PassengerId',axis=1, inplace=True)

Divide into training and tets sets

When we test a machine learning model we should always test it on data that has not been used to train the model. We will use sklearn’s train_test_split method to randomly split the data: 75% for training, and 25% for testing.

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42, test_size=0.25)

Standardise data

Use SciKit learn method for standardising data.

def standardise_data(X_train, X_test):
    
    # Initialise a new scaling object for normalising input data
    sc = StandardScaler() 

    # Set up the scaler just on the training set
    sc.fit(X_train)

    # Apply the scaler to the training and test sets
    train_std=sc.transform(X_train)
    test_std=sc.transform(X_test)
    
    return train_std, test_std

X_train_std, X_test_std = standardise_data(X_train, X_test)

Fit logistic regression model

Now we will fir a logistic regression model, using sklearn’s LogisticRegression method.

model = LogisticRegression(random_state=42)
model.fit(X_train_std,y_train)

LogisticRegression(random_state=42)

Predict values and get probabilities of survival

Now we can use the trained model to predict survival. We will test the accuracy of both the training and test data sets.

# Predict training and test set labels
y_pred_train = model.predict(X_train_std)
y_pred_test = model.predict(X_test_std)

# Predict probabilities of survival
y_prob_train = model.predict_proba(X_train_std)
y_prob_test = model.predict_proba(X_test_std)

Calculate accuracy

In this example we will measure accuracy simply as the proportion of passengers where we make the correct prediction. In a later notebook we will look at other measures of accuracy which explore false positives and false negatives in more detail.

accuracy_train = np.mean(y_pred_train == y_train)
accuracy_test = np.mean(y_pred_test == y_test)

print (f'Accuracy of predicting training data = {accuracy_train:0.3f}')
print (f'Accuracy of predicting test data = {accuracy_test:0.3f}')

Accuracy of predicting training data = 0.808
Accuracy of predicting test data = 0.798

Examining the model coefficients (weights)

# Get model co_efficients
co_eff = model.coef_[0]

# Put in DataFrame and sort by effect size
co_eff_df = pd.DataFrame()
co_eff_df['feature'] = list(X) # Get feature names from X
co_eff_df['co_eff'] = co_eff
co_eff_df['abs_co_eff'] = np.abs(co_eff)
co_eff_df_sorted = \
    co_eff_df.sort_values(by='abs_co_eff', ascending=False, inplace=False)

co_eff_df_sorted.head()

	feature	co_eff	abs_co_eff
10	male	-1.285766	1.285766
0	Pclass	-0.599109	0.599109
1	Age	-0.443450	0.443450
9	CabinNumberImputed	-0.383161	0.383161
2	SibSp	-0.326892	0.326892

The three most influential features are:

• male (being male reduces probability of survival)

• Pclass (lower class passengers, who have a higher class number, reduces probability of survival)

• age (being older reduces probability of survival)

Get Shapley values

We use the shap_values method from the SHAP library to get Shapley values. We use the explainer method from the SHAP library to get Shapley values along with other data.

# Get list of features
features = list(X_train)

# Train explainer on Training set
explainer = shap.Explainer(model, X_train_std)
    
# Get Shap values (extended version has other data returned as well as shap values)
shapley_values_train = explainer.shap_values(X_train_std)
shapley_values_train_extended = explainer(X_train_std)
shapley_values_test = explainer.shap_values(X_test_std)
shapley_values_test_extended = explainer(X_test_std)

# Calculate mean Shapley value for each feature in trainign set
co_eff_df['mean_shapley_values'] = shapley_values_train.mean(axis=0)

# Calculate mean absolute Shapley value for each feature in trainign set
# This will give us the average importance of each feature
co_eff_df['mean_abs_shapley_values'] = np.mean(
    np.abs(shapley_values_train),axis=0)

Add Shapley values to coefficient table.

co_eff_df.sort_values(by='abs_co_eff', ascending=False).head()
co_eff_df.head(10)

	feature	co_eff	abs_co_eff	mean_shapley_values	mean_abs_shapley_values
0	Pclass	-0.599109	0.599109	-0.075577	0.553688
1	Age	-0.443450	0.443450	0.021086	0.321889
2	SibSp	-0.326892	0.326892	0.021006	0.215346
3	Parch	-0.120718	0.120718	0.008693	0.091400
4	Fare	0.201812	0.201812	0.017323	0.103516
5	AgeImputed	-0.209965	0.209965	-0.025102	0.152032
6	EmbarkedImputed	0.098489	0.098489	0.005397	0.005397
7	CabinLetterImputed	0.080356	0.080356	0.010992	0.072992
8	CabinNumber	0.121569	0.121569	-0.021160	0.092512
9	CabinNumberImputed	-0.383161	0.383161	-0.061586	0.349546

Get top 10 influenctial features by co-effieceints or Shapley

# Get top 10 features
co_eff_top_10 = \
    co_eff_df.sort_values(by='abs_co_eff', ascending=False).head(10)['feature']

shapley_top_10 = \
    co_eff_df.sort_values(
    by='mean_abs_shapley_values', ascending=False).head(10)['feature']

# Add to DataFrame
top_10_features = pd.DataFrame()
top_10_features['Coefficients'] = co_eff_top_10.values
top_10_features['Shapley'] = shapley_top_10.values

# Display
top_10_features

	Coefficients	Shapley
0	male	male
1	Pclass	Pclass
2	Age	CabinNumberImputed
3	CabinNumberImputed	Age
4	SibSp	SibSp
5	CabinLetter_C	AgeImputed
6	AgeImputed	CabinLetter_C
7	Fare	Embarked_S
8	CabinLetter_E	Fare
9	CabinLetter_T	CabinLetter_E

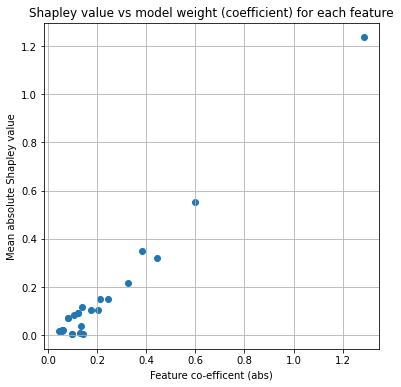
We can see a lot of overlap between the most import fatures as estimated by coefficients and those estimated using mean absolute Shapley values. But they are not identical.

Plot comparison of Shapley and model coefficients:

fig = plt.figure(figsize=(6,6))
ax = fig.add_subplot(111)
# Plot points
x = co_eff_df['abs_co_eff']
y = co_eff_df['mean_abs_shapley_values']
ax.scatter(x, y)
ax.set_title('Shapley value vs model weight (coefficient) for each feature')
ax.set_ylabel('Mean absolute Shapley value')
ax.set_xlabel('Feature co-efficent (abs)')
plt.grid()
plt.show()

Plots of Shapley values

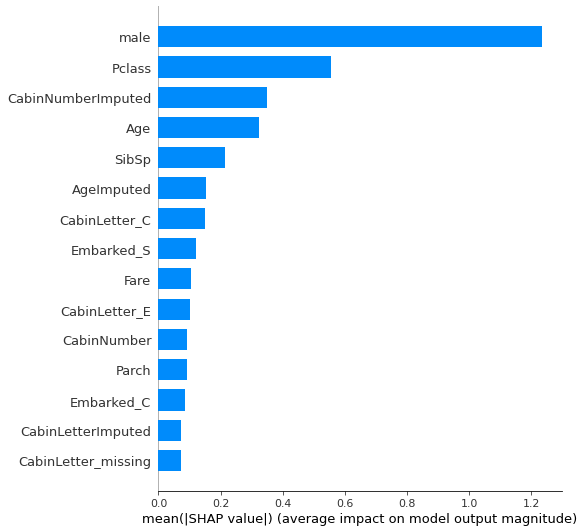
Summary plot

The summary_plot using a plot_type option of bar gives us the overall importance of each feature across the population.

Here we limit the num,ber of features shown to 15 (default is 20).

fig = plt.figure(figsize=(6,6))

shap.summary_plot(shap_values = shapley_values_train, 
                  features = X_train.values,
                  feature_names = X_train.columns.values,
                  plot_type='bar',
                  max_display=15,
                  show=False)
plt.tight_layout()
plt.show()

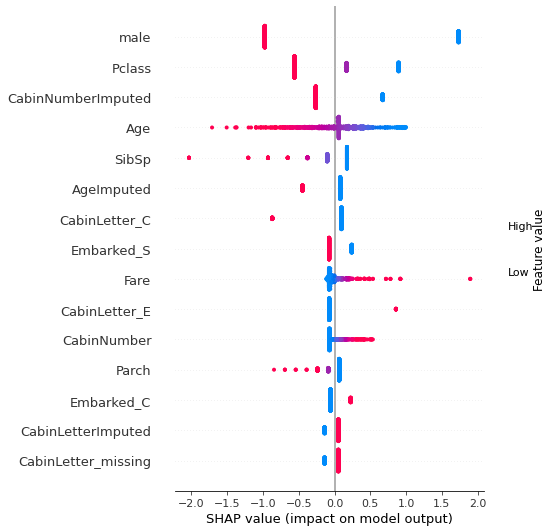
Beeswarm plot

Without specifying a plot_type option of bar, summary_plot gives us a beeswarm plot, showing the Shapley values for all instances.

fig = plt.figure(figsize=(6,6))

shap.summary_plot(shap_values = shapley_values_train, 
                  features = X_train.values,
                  feature_names = X_train.columns.values,
                  max_display=15,
                  show=False)
plt.tight_layout()
plt.show()

Waterfall plot

Waterfall plots show the influence of individual features on model prediction. These are shown as the effect on log odds ratio of survival. Log odds ratio are usually shown as these are additive, whereas probabilities are not.

Waterfall plots put the most influential features at the top.

Waterfall plot for passenger with lowest probability of survival:

y_probs = model.predict_proba(X_test_std)

# For waterfall plot with feature names shap needs a df with feature names
df = pd.DataFrame(X_test_std, columns=list(X_train))

# Fit explainer model and get Shap values
explainer = shap.Explainer(model, df)
shap_values = explainer(df)

# Get probability of survival
y_probs_survive = model.predict_proba(df)[:,1]
# Get index of lowest survival probability
location_low_probability = np.where(y_probs == y_probs_survive.min())[0][0]

# Waterfall plot
shap.plots.waterfall(shap_values[location_low_probability], max_display=15)

X has feature names, but LogisticRegression was fitted without feature names

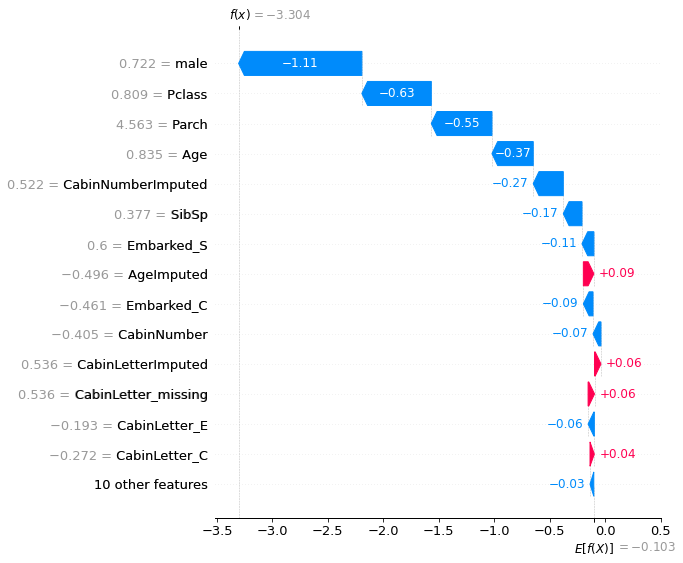
Waterfall plot for passenger with highest probability of survival:

# Get index of lowest survival probability
location_high_probability = np.where(y_probs == y_probs_survive.max())[0][0]

# Waterfall plot
shap.plots.waterfall(shap_values[location_high_probability], max_display=15)

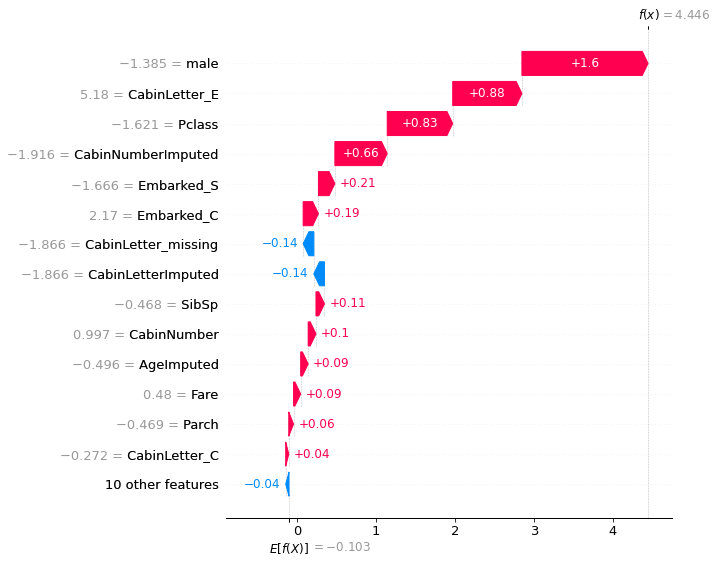
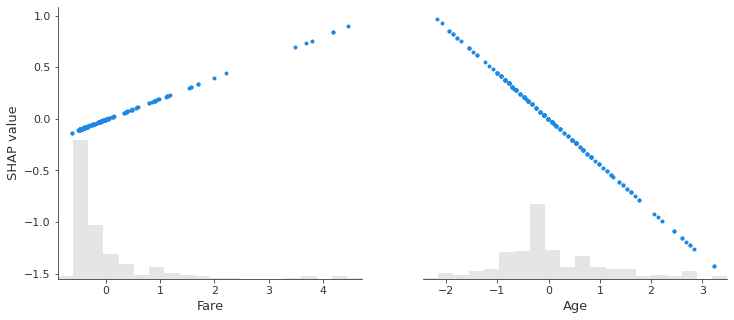
Scatter plot

A scattter plot for one or more features shows the relationship between the feature value and the Shap value, along with a histogram of the frequency of the feature values.

shap.plots.scatter(shap_values[:,['Fare', 'Age']])