Random Forest Receiver Operator Characteristic (ROC) curve and balancing of model classification
Contents
Random Forest Receiver Operator Characteristic (ROC) curve and balancing of model classification#
In this model we apply ROC to a Random Forest model. As these components have been previously described, we’ll keep comments to a minimum.
# Hide warnings (to keep notebook tidy; do not usually do this)
import warnings
warnings.filterwarnings("ignore")
Load modules#
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import auc
from sklearn.model_selection import StratifiedKFold
Download data if not previously downloaded#
download_required = True
if download_required:
# Download processed data:
address = 'https://raw.githubusercontent.com/MichaelAllen1966/' + \
'1804_python_healthcare/master/titanic/data/processed_data.csv'
data = pd.read_csv(address)
# Create a data subfolder if one does not already exist
import os
data_directory ='./data/'
if not os.path.exists(data_directory):
os.makedirs(data_directory)
# Save data
data.to_csv(data_directory + 'processed_data.csv', index=False)
Define function to calculate accuracy measurements#
import numpy as np
def calculate_accuracy(observed, predicted):
"""
Calculates a range of accuracy scores from observed and predicted classes.
Takes two list or NumPy arrays (observed class values, and predicted class
values), and returns a dictionary of results.
1) observed positive rate: proportion of observed cases that are +ve
2) Predicted positive rate: proportion of predicted cases that are +ve
3) observed negative rate: proportion of observed cases that are -ve
4) Predicted negative rate: proportion of predicted cases that are -ve
5) accuracy: proportion of predicted results that are correct
6) precision: proportion of predicted +ve that are correct
7) recall: proportion of true +ve correctly identified
8) f1: harmonic mean of precision and recall
9) sensitivity: Same as recall
10) specificity: Proportion of true -ve identified:
11) positive likelihood: increased probability of true +ve if test +ve
12) negative likelihood: reduced probability of true +ve if test -ve
13) false positive rate: proportion of false +ves in true -ve patients
14) false negative rate: proportion of false -ves in true +ve patients
15) true positive rate: Same as recall
16) true negative rate: Same as specificity
17) positive predictive value: chance of true +ve if test +ve
18) negative predictive value: chance of true -ve if test -ve
"""
# Converts list to NumPy arrays
if type(observed) == list:
observed = np.array(observed)
if type(predicted) == list:
predicted = np.array(predicted)
# Calculate accuracy scores
observed_positives = observed == 1
observed_negatives = observed == 0
predicted_positives = predicted == 1
predicted_negatives = predicted == 0
true_positives = (predicted_positives == 1) & (observed_positives == 1)
false_positives = (predicted_positives == 1) & (observed_positives == 0)
true_negatives = (predicted_negatives == 1) & (observed_negatives == 1)
false_negatives = (predicted_negatives == 1) & (observed_negatives == 0)
accuracy = np.mean(predicted == observed)
precision = (np.sum(true_positives) /
(np.sum(true_positives) + np.sum(false_positives)))
recall = np.sum(true_positives) / np.sum(observed_positives)
sensitivity = recall
f1 = 2 * ((precision * recall) / (precision + recall))
specificity = np.sum(true_negatives) / np.sum(observed_negatives)
positive_likelihood = sensitivity / (1 - specificity)
negative_likelihood = (1 - sensitivity) / specificity
false_positive_rate = 1 - specificity
false_negative_rate = 1 - sensitivity
true_positive_rate = sensitivity
true_negative_rate = specificity
positive_predictive_value = (np.sum(true_positives) /
(np.sum(true_positives) + np.sum(false_positives)))
negative_predictive_value = (np.sum(true_negatives) /
(np.sum(true_negatives) + np.sum(false_negatives)))
# Create dictionary for results, and add results
results = dict()
results['observed_positive_rate'] = np.mean(observed_positives)
results['observed_negative_rate'] = np.mean(observed_negatives)
results['predicted_positive_rate'] = np.mean(predicted_positives)
results['predicted_negative_rate'] = np.mean(predicted_negatives)
results['accuracy'] = accuracy
results['precision'] = precision
results['recall'] = recall
results['f1'] = f1
results['sensitivity'] = sensitivity
results['specificity'] = specificity
results['positive_likelihood'] = positive_likelihood
results['negative_likelihood'] = negative_likelihood
results['false_positive_rate'] = false_positive_rate
results['false_negative_rate'] = false_negative_rate
results['true_positive_rate'] = true_positive_rate
results['true_negative_rate'] = true_negative_rate
results['positive_predictive_value'] = positive_predictive_value
results['negative_predictive_value'] = negative_predictive_value
return results
Load data#
data = pd.read_csv('data/processed_data.csv')
# Make all data 'float' type
data = data.astype(float)
data.drop('PassengerId', inplace=True, axis=1)
X = data.drop('Survived',axis=1) # X = all 'data' except the 'survived' column
y = data['Survived'] # y = 'survived' column from 'data'
# Convert to NumPy as required for k-fold splits
X_np = X.values
y_np = y.values
Run model and collect results#
# Set up k-fold training/test splits
number_of_splits = 5
skf = StratifiedKFold(n_splits = number_of_splits)
skf.get_n_splits(X_np, y_np)
# Set up thresholds
thresholds = np.arange(0, 1.01, 0.01)
# Create arrays for overall results (rows=threshold, columns=k fold replicate)
results_accuracy = np.zeros((len(thresholds),number_of_splits))
results_precision = np.zeros((len(thresholds),number_of_splits))
results_recall = np.zeros((len(thresholds),number_of_splits))
results_f1 = np.zeros((len(thresholds),number_of_splits))
results_predicted_positive_rate = np.zeros((len(thresholds),number_of_splits))
results_observed_positive_rate = np.zeros((len(thresholds),number_of_splits))
results_true_positive_rate = np.zeros((len(thresholds),number_of_splits))
results_false_positive_rate = np.zeros((len(thresholds),number_of_splits))
results_auc = []
# Loop through the k-fold splits
loop_index = 0
for train_index, test_index in skf.split(X_np, y_np):
# Create lists for k-fold results
threshold_accuracy = []
threshold_precision = []
threshold_recall = []
threshold_f1 = []
threshold_predicted_positive_rate = []
threshold_observed_positive_rate = []
threshold_true_positive_rate = []
threshold_false_positive_rate = []
# Get X and Y train/test
X_train, X_test = X_np[train_index], X_np[test_index]
y_train, y_test = y_np[train_index], y_np[test_index]
# Set up and fit model (n_jobs=-1 uses all cores on a computer)
model = RandomForestClassifier(n_jobs=-1)
model.fit(X_train,y_train)
# Get probability of non-survive and survive
probabilities = model.predict_proba(X_test)
# Take just the survival probabilities (column 1)
probability_survival = probabilities[:,1]
# Loop through increments in probability of survival
for cutoff in thresholds: # loop 0 --> 1 on steps of 0.1
# Get whether passengers survive using cutoff
predicted_survived = probability_survival >= cutoff
# Call accuracy measures function
accuracy = calculate_accuracy(y_test, predicted_survived)
# Add accuracy scores to lists
threshold_accuracy.append(accuracy['accuracy'])
threshold_precision.append(accuracy['precision'])
threshold_recall.append(accuracy['recall'])
threshold_f1.append(accuracy['f1'])
threshold_predicted_positive_rate.append(
accuracy['predicted_positive_rate'])
threshold_observed_positive_rate.append(
accuracy['observed_positive_rate'])
threshold_true_positive_rate.append(accuracy['true_positive_rate'])
threshold_false_positive_rate.append(accuracy['false_positive_rate'])
# Add results to results arrays
results_accuracy[:,loop_index] = threshold_accuracy
results_precision[:, loop_index] = threshold_precision
results_recall[:, loop_index] = threshold_recall
results_f1[:, loop_index] = threshold_f1
results_predicted_positive_rate[:, loop_index] = \
threshold_predicted_positive_rate
results_observed_positive_rate[:, loop_index] = \
threshold_observed_positive_rate
results_true_positive_rate[:, loop_index] = threshold_true_positive_rate
results_false_positive_rate[:, loop_index] = threshold_false_positive_rate
# Calculate ROC AUC
roc_auc = auc(threshold_false_positive_rate, threshold_true_positive_rate)
results_auc.append(roc_auc)
# Increment loop index
loop_index += 1
# Transfer summary results to dataframe
results = pd.DataFrame(thresholds, columns=['thresholds'])
results['accuracy'] = results_accuracy.mean(axis=1)
results['precision'] = results_precision.mean(axis=1)
results['recall'] = results_recall.mean(axis=1)
results['f1'] = results_f1.mean(axis=1)
results['predicted_positive_rate'] = \
results_predicted_positive_rate.mean(axis=1)
results['observed_positive_rate'] = \
results_observed_positive_rate.mean(axis=1)
results['true_positive_rate'] = results_true_positive_rate.mean(axis=1)
results['false_positive_rate'] = results_false_positive_rate.mean(axis=1)
results['roc_auc'] = np.mean(results_auc)
mean_auc = np.mean(results_auc)
mean_auc = np.round(mean_auc, 3)
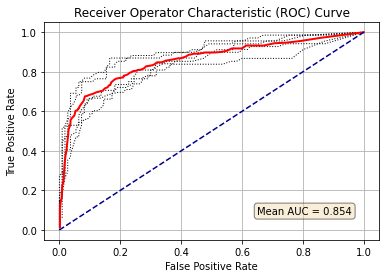
Plot ROC curve#
for i in range(number_of_splits):
plt.plot(results_false_positive_rate[:, i],
results_true_positive_rate[:, i],
color='black',
linestyle=':',
linewidth=1)
plt.plot(results_false_positive_rate.mean(axis=1),
results_true_positive_rate.mean(axis=1),
color='red',
linestyle='-',
linewidth=2)
plt.plot([0, 1], [0, 1], color='darkblue', linestyle='--')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operator Characteristic (ROC) Curve')
plt.grid(True)
props = dict(boxstyle='round', facecolor='wheat', alpha=0.5)
text = "Mean AUC = " + str(mean_auc)
plt.text(0.65, 0.08, text, bbox=props)
plt.show()
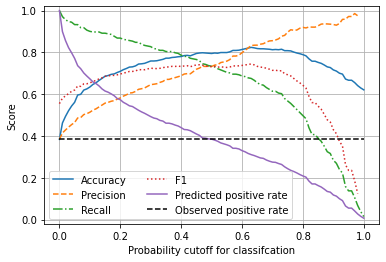
Plot effects of changing classification probability threshold#
chart_x = results['thresholds']
plt.plot(chart_x, results['accuracy'],
linestyle = '-',
label = 'Accuracy')
plt.plot(chart_x, results['precision'],
linestyle = '--',
label = 'Precision')
plt.plot(chart_x, results['recall'],
linestyle = '-.',
label = 'Recall')
plt.plot(chart_x, results['f1'],
linestyle = ':',
label = 'F1')
plt.plot(chart_x, results['predicted_positive_rate'],
linestyle = '-',
label = 'Predicted positive rate')
plt.plot(chart_x, results['observed_positive_rate'],
linestyle = '--',
color='k',
label = 'Observed positive rate')
plt.xlabel('Probability cutoff for classifcation')
plt.ylabel('Score')
plt.ylim(-0.02, 1.02)
plt.legend(loc='lower left', ncol=2)
plt.grid(True)
plt.show()
Observations#
The Random Forest model, with default settings, has an ROC AUC of 0.85.
Unlike the logistic regression model, the default probability threshold of 0.5 produces a balanced model, where precision = recall, and where the predicted survival rate is the same as the observed survival rate.
If needed, the probability threshold of the Random Forest model could be adjust to change the model characteristics, such as for use in screening where recall (the detection of true positives) needs to be minimised at the accepted cost of lower precision (the detection of true negatives). In a screening situation false positives are generally accepted (as they will be eliminated later), but false negatives (where a condition is missed in screening) is much less acceptable.
You will see that many aspects of machine learning models are directly transferable between model types.